今天的题目是LeetCode 2039. 网络空闲的时刻，令我产生多个思考，来看题目。

题目

给你一个有 n 个服务器的计算机网络，服务器编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示服务器 ui 和 vi 之间有一条信息线路，在一秒内它们之间可以传输任意数目的信息。再给你一个长度为 n 且下标从 0 开始的整数数组 patience 。

题目保证所有服务器都是相通的，也就是说一个信息从任意服务器出发，都可以通过这些信息线路直接或间接地到达任何其他服务器。

编号为 0 的服务器是主服务器，其他服务器为数据服务器。每个数据服务器都要向主服务器发送信息，并等待回复。信息在服务器之间按 最优线路 传输，也就是说每个信息都会以 最少时间 到达主服务器。主服务器会处理所有新到达的信息并立即按照每条信息来时的路线 反方向 发送回复信息。

在 0 秒的开始，所有数据服务器都会发送各自需要处理的信息。从第 1 秒开始，每一秒最开始时，每个数据服务器都会检查它是否收到了主服务器的回复信息（包括新发出信息的回复信息）：

如果还没收到任何回复信息，那么该服务器会周期性重发信息。数据服务器 i 每 patience[i] 秒都会重发一条信息，也就是说，数据服务器 i 在上一次发送信息给主服务器后的 patience[i] 秒后会重发一条信息给主服务器。
否则，该数据服务器 不会重发 信息。

当没有任何信息在线路上传输或者到达某服务器时，该计算机网络变为空闲状态。

请返回计算机网络变为空闲状态的 最早秒数 。

示例

示例1：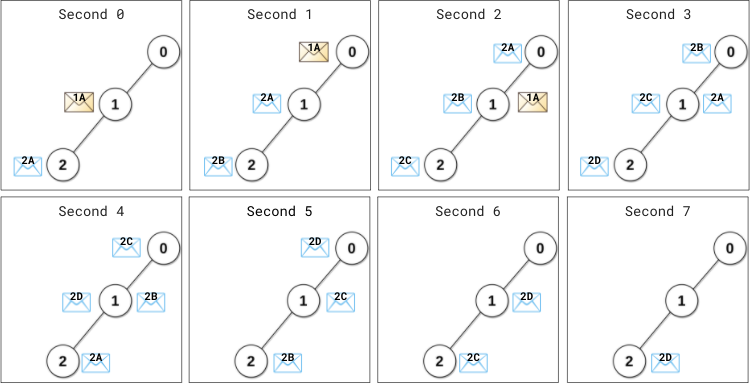
来自LeetCode

输入：edges = [[0,1],[1,2]], patience = [0,2,1]
输出：8
解释：
0 秒最开始时，
- 数据服务器 1 给主服务器发出信息（用 1A 表示）。
- 数据服务器 2 给主服务器发出信息（用 2A 表示）。

1 秒时，
- 信息 1A 到达主服务器，主服务器立刻处理信息 1A 并发出 1A 的回复信息。
- 数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒（1 < patience[1] = 2），所以不会重发信息。
- 数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒（1 == patience[2] = 1），所以它重发一条信息（用 2B 表示）。

2 秒时，
- 回复信息 1A 到达服务器 1 ，服务器 1 不会再重发信息。
- 信息 2A 到达主服务器，主服务器立刻处理信息 2A 并发出 2A 的回复信息。
- 服务器 2 重发一条信息（用 2C 表示）。
...
4 秒时，
- 回复信息 2A 到达服务器 2 ，服务器 2 不会再重发信息。
...
7 秒时，回复信息 2D 到达服务器 2 。

从第 8 秒开始，不再有任何信息在服务器之间传输，也不再有信息到达服务器。
所以第 8 秒是网络变空闲的最早时刻。

示例2：
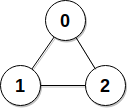
leetCode

输入：edges = [[0,1],[0,2],[1,2]], patience = [0,10,10]
输出：3
解释：数据服务器 1 和 2 第 2 秒初收到回复信息。
从第 3 秒开始，网络变空闲。

题解

今天的题目那是十分之长，看吐了，谢谢你 LeetCode。

看完后第一反应就是广搜（BFS），从主服务器 0 开始向四周搜索所有子服务器的 最短路径 。

如果不理解广搜可以先看看我以前的BFS相关文章 LeetCode每日一题 1034. 边界着色

获得最短路径之后我们开始计算每一个服务器从 第一次 发信到 最后一次 收到回信之间的时间，在这些服务器中耗时最长的即是本题答案：“计算机网络变为空闲状态的 最早秒数 ” 。

我们已知服务器 n 的重复发信周期为 patience[n] 秒，以及通过上文提到的搜索计算出来的服务器 n 到服务器 n 的最短通信时间 server_time 秒。

这里会分为两种情况：

patience[n] >= server_time：当服务器 n 收到它第一次发信的回信后，重复发信周期还未到；或是因为收信优先级高于发信，还没来得及发信就收到了第一次的发信，打断了下一次的发信，这个时候就已经完成了这个服务器的整个收发动作，网络中也不再存在来自此服务器的数据或是发送给此服务器的数据，则一次收发动作 server_time*2 + 1 就是服务器 n 的整个 “变为空闲状态的最早秒数”。
patience[n] < server_time：当服务器 n 还未收到它第一次发信的回信时就已触发了重复发信周期，这个时候在它收到第一次发信的回信后，整个网络中还存在着 (time * 2-1) /patience[n] 个关于这个服务器 n 的数据，此时这个服务器还将继续收信不能变为空闲状态，所以当达到服务器 n 的整个 “变为空闲状态的最早秒数” 应该是 server_time*2 + patience[n]*((time * 2-1) /patience[n]) + 1。

然而当 patience[n] >= server_time 时 patience[n]*((time * 2-1) /patience[n])==0, 所以以上两个条件的公式可以复用为 server_time*2 + patience[n]*((time * 2-1) /patience[n]) + 1。

由于本人思路不及他人，所以以上题解思路来自于 LeetCode 官方题解，如果您有兴趣看一看我的思路请翻到我的思路。

开始写代码吧。

代码

// 执行 680 ms 超越 9.48%  消耗 198.4 MB 超越 26.72%
class Solution {
public:
    int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
        vector<bool> visit(patience.size(),false);
        vector<vector<int>> edges_map(patience.size());
        for(auto i:edges)
        {
            edges_map[i[0]].push_back(i[1]);
            edges_map[i[1]].push_back(i[0]);
        }
        queue<int> que;
        que.push(0);
        visit[0]=true; //主服务器去除
        int max_time=0;
        int time=1;
        while(!que.empty())
        {
            int qsize=que.size();
            for(int j=0;j<qsize;j++)
            {
                for(int i:edges_map[que.front()])
                {
                    if(!visit[i])
                    {
                        que.emplace(i);
                        max_time=max(time*2 + patience[i]*((time*2-1) / patience[i]),max_time);
                        visit[i]=true;
                    }
                }
                que.pop();
            }
            time++;
        }
        return max_time+1;
    }
};

PS

我的思路

理解官方思路后重新写了代码，但都无法追上官方的成绩，思考了一下午的时间，还是放弃……如果有大佬路过看到此篇能提供帮助小辈万分感谢。

实际上我的思路与官方的大差不差，但在实现方法上有不同。
来看整个代码：

class Solution {
public:
    map<int,set<int>> edges_map;  //使用map与set会浪费空间，所以尽量使用vector
    vector<int> server_lenght;
    int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& patience) {
        server_lenght.resize(patience.size());
        for(auto i:edges)
        {
            edges_map[i[0]].insert(i[1]);
            edges_map[i[1]].insert(i[0]);
        }
        int max_time=0;
        find_server(0,0);
        for(int i=1;i<server_lenght.size();i++)
        {
            if(server_lenght[i]*2 % patience[i] == 0)
                max_time = max(server_lenght[i]*4 - patience[i],max_time);
                //从第0秒开始发信，到第 server_lenght[i]*2 秒收到回信时，此服务器最后一条信息已开始 server_lenght[i]*2 % patience[i] 秒
            else if(server_lenght[i]*2 > patience[i])
                max_time = max(server_lenght[i]*4 - (server_lenght[i]*2 % patience[i]),max_time);
                //当出现 server_lenght[i]*2 % patience[i] == 0 条件时服务器的第一次发信已收到回信，则还在第 0 秒的最后一条发信停止发信
            else
                max_time = max(server_lenght[i]*2,max_time);
                //如果 patience[i] > server_lenght[i]*2 , 此时服务器还尚未发信
            cout<<server_lenght[i]<<endl;
        }  
        return max_time+1;
    }
    void find_server(int n,int sl)
    {
        for(auto i:edges_map[n])
        {
            if(server_lenght[i]<=sl+1 && server_lenght[i]!=0) //防止回环
                continue;
            if(server_lenght[i]==0 || server_lenght[i]>sl+1)
                server_lenght[i]=sl+1;
            find_server(i,sl+1);
        }
    }
};