LeetCode每日一题 1034. 边界着色

今天的每日一题是LeetCode每日一题 1034. 边界着色。

来看题目。

题目

给你一个大小为 m x n 的整数矩阵 grid ，表示一个网格。另给你三个整数 row、col 和 color 。网格中的每个值表示该位置处的网格块的颜色。

当两个网格块的颜色相同，而且在四个方向中任意一个方向上相邻时，它们属于同一连通分量。

连通分量的边界是指连通分量中的所有与不在分量中的网格块相邻（四个方向上）的所有网格块，或者在网格的边界上（第一行/列或最后一行/列）的所有网格块。

请你使用指定颜色 color 为所有包含网格块 grid[row][col] 的连通分量的边界进行着色，并返回最终的网格grid 。

题解

老实说题目翻译得不准确，我看了许久还是翻了翻评论区，终于知道是什么意思。

题目的意思是给你个矩阵grid，然后在矩阵中指定一个元素grid[row][col]出来作为基准，让我们找这个元素的数字的连通分量的最大范围，并且还要在边界处涂上颜色Color，画个图理解一下。
例如矩阵grid长这样，指定的元素为gird[2][2]=2，color=3。

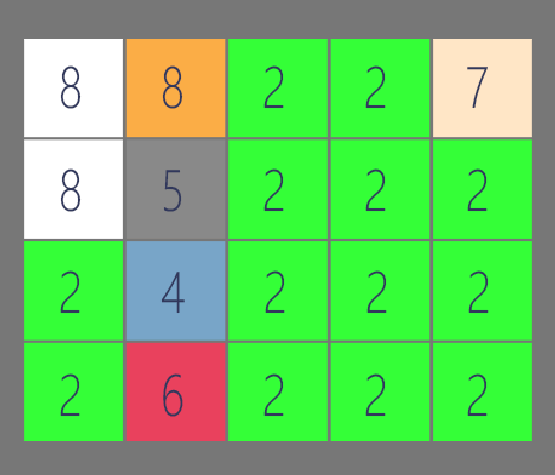
那么我们可以知道2的最大连通分量区间为

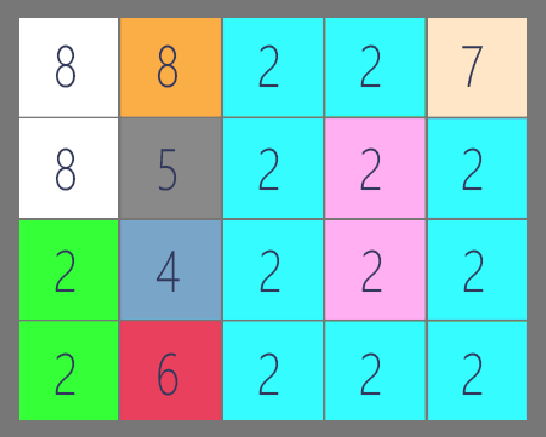
为连通分量的边界换上color=3,即返回结果

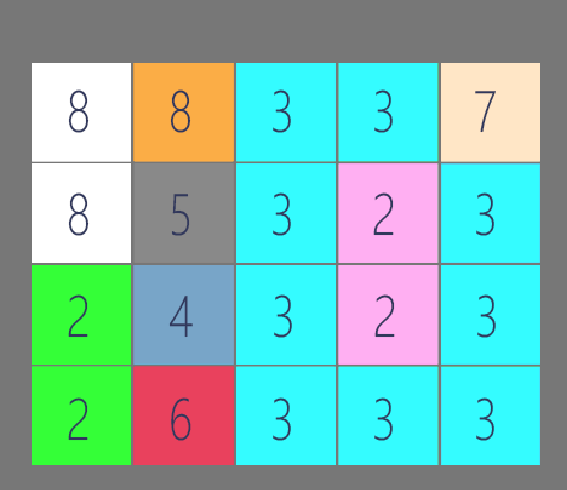
那么我们要如何找到 grid[row][col] 的最大连通分量区间呢？很明显，使用搜索。
本篇展示的是广度搜索(BFS),这道题当然也能使用深度搜索(DFS)来计算，您可以自己尝试编写算法。

我们以 grid[row][col] 为起点开始搜索以 grid[row][col] 为中心的连通分量区。

符合作为grid[row][col]元素的连通分量有的特征是与上下左右四面相邻的方块至少一块“颜色”（即数据）相同。

符合作为grid[row][col]元素的连通分量边界的特征：第一要是一个连通变量并且“颜色”与grid相同且处于一个区内，第二个是与一定与其他“颜色”为邻，像这样的连通分量我们要为它涂上“颜色”Color。

所以程序运行的流程逻辑分为以下几点。

1、判断 grid[i][j] 是否为与 grid[row][col] 相同的连通分量，是就改为0，防止在同一位置重复运行导致死循环。

2、判断 grid[i][j] 是否为连通分量边界，为了防止相邻元素判断时与更换后连通分量边界元素发生判断性错误，改为-grid[row][col] 。

3、使用递归访问 grid[i][j] 的上下左右节点，重复1，2，3过程。

PS：
在我的代码中，拥有一个vector<vector> G = grid,它与grid进行同步修改，在grid[i][j]改成-grid[row][col]时直接向G[i][j]“染色”。完成流程后直接返回G即可。

弄了个GIF，让大家能够快速理解。

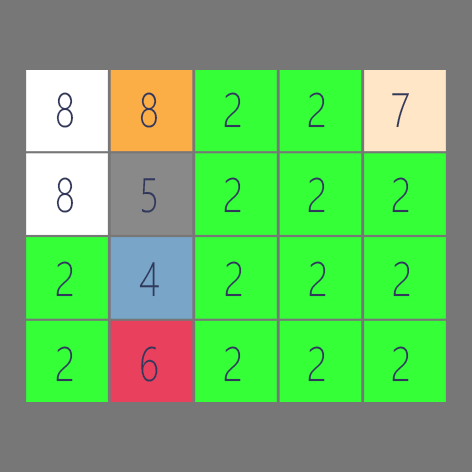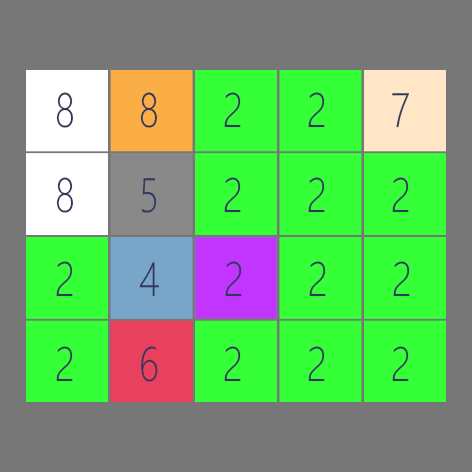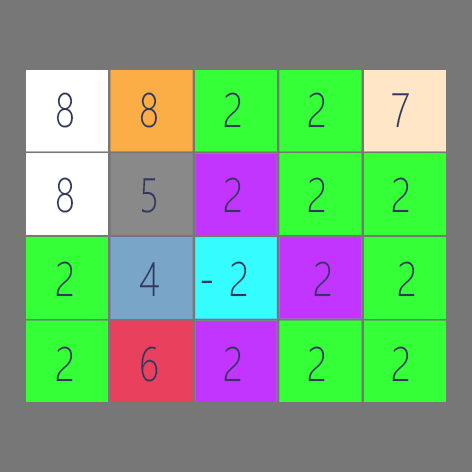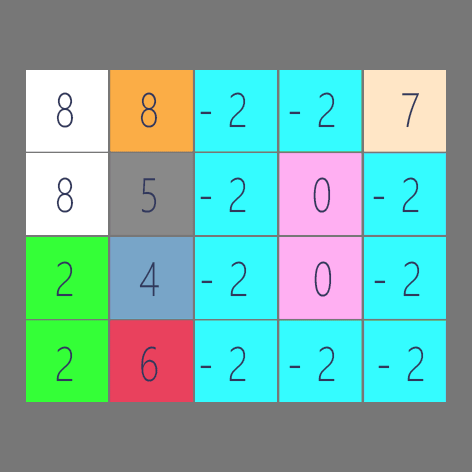
那么让我们开始码代码吧。

代码示例

class Solution {
public:
    int col_co=0;
    int Color=0;
    vector<vector<int>> G;
    vector<vector<int>> colorBorder(vector<vector<int>>& grid, int row, int col, int color) {
        col_co=grid[row][col];
        Color=color;
        G=grid;
        find(grid,row,col);
        return G;
    }
    void find(vector<vector<int>> &grid,int i, int j)
    {
        if( i<0 || j<0 || i>=grid.size() || j>=grid[0].size())
            return;
        
        if(grid[i][j]==0 || abs(grid[i][j])!=col_co)
            return;
        if(grid[i][j]==col_co)
        {
            if( i==0 || j==0 || i==grid.size()-1 || j==grid[0].size()-1 )
                G[i][j]=Color,grid[i][j]=-col_co;
            else if( (i-1>=0 && j-1>=0 && i+1<grid.size() && j+1<grid[0].size()) && 
           ((abs(grid[i-1][j])!=col_co && grid[i-1][j]!=0 ) || 
            (abs(grid[i+1][j])!=col_co && grid[i+1][j]!=0 ) || 
            (abs(grid[i][j-1])!=col_co && grid[i][j-1]!=0 ) || 
            (abs(grid[i][j+1])!=col_co && grid[i][j+1]!=0 ) ) 
            )
                G[i][j]=Color,grid[i][j]=-col_co;
            else
                grid[i][j]=0;
            find(grid,i+1,j);
            find(grid,i-1,j);
            find(grid,i,j+1);
            find(grid,i,j-1);
        }
    }
};